在對結構進行有限元分析時,結構
材料的工程常數是一組非常重要的特性參數。必須確保程序輸入的材料的工程常數的準確性,才能保證有限元分析結果的正確性和有效性。對于簡單的各向同性材料,可看作每一個平面都是對稱面,每一個方向都是彈性對稱軸,也即其體內每一點的任意方向上的彈性性質都相同。因此,對于各向同性材料,彈性常數對任意正交坐標系是不變的。而各向異性材料最突出的特點,就是它的方向性,各向異性材料的彈性系數是方向的函數,它們和坐標的取向有關。
在利用ANSYS有限元程序對纖維增強
復合材料氣瓶進行應力分析時,遇到了如何正確確定復合材料彈性常數的問題。因為多層復合材料纏繞結構中,不同的纏繞層有不同的纏繞方向,也就是不同的纖維纏繞層有不同的材料坐標系。而復合材料與均質各向同性材料的主要本質差別在于:即使在宏觀上看,也會呈現出明顯的非均質各向異性,尤其纖維增強復合材料的各向異性特性顯得更加強烈。即纖維增強復合材料在不同的坐標方向上有不同的彈性特性。

通過材料實驗所得到的是材料主軸坐標方向上的彈性系數值,而利用ANSYS進行有限元分析時,程序要求輸入的是與系統整體的求解坐標系相一致的彈性參數。因此,對于有著不同纏繞方向的多層復合材料來說,存在將彈性系數由材料主軸坐標系向系統整體坐標系進行轉換的問題。這種轉換并不是實際物理意義上的轉換,而是一種為簡化分析過程的等效參數轉換,因此其正確性需要實際計算的驗證。
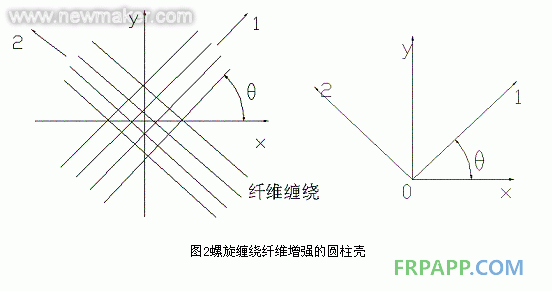
利用ANSYS的結構非線性分析功能,對一復合材料纏繞殼體進行應力分析。殼體模型為一六層結構,最內層為鋁內膽層,外層為連續五層的復合材料纏繞層,前三層為
碳纖維纏繞層,纏繞方向分別為環纏、螺旋纏和高角纏繞;后兩層為玻纖纏繞層,纏繞方向分別為螺旋纏繞和環向纏繞。由于殼體的對稱性結構,因此選用ANSYS的軸對稱單元對其進行分析。殼體施加內壓載荷作用。

計算出不同纏繞方向材料坐標系上的工程常數轉換到統一的整體坐標系上的等效的工程常數,然后按不同層分別輸入不同的工程常數值,利用ANSYS的非線性功能分別在不同內壓載荷作用下進行求解,最后得到各個層的應力值分布。

由圖可以看出,每個單層內部的應力水平接近,而不同層間的應力具有不同的應力水平;這種應力的分布規律也是符合纖維的不同纏繞方向的。用ANSYS分析的結果和與實驗所得結果進行比較,其吻合程度較好。因此,這就充分證明,對于材料主軸方向不一致的各向異性材料組成的這種層狀結構,利用坐標變換的方法對其工程常數進行等效變換是可行的



















 魯ICP備2021047099號
魯ICP備2021047099號